
Filip Rindler - Space-time integral currents of bounded variation
Published at : October 09, 2021
Filip Rindler (Warwick U) - Space-time integral currents of bounded variation
I will present aspects of a theory of space-time integral currents
with bounded variation in time. This is motivated by a recent model
for elasto-plastic evolutions that are driven by the flow of
dislocations (this model is joint work with T. Hudson). The classical
scalar BV-theory can be recovered as the 0-dimensional limit case of
this BV space-time theory. However, the emphasis is on evolutions of
higher-dimensional objects, most notably 1D loops moving within 3D
domains (i.e., the codimension 2 case), which corresponds to
dislocation dynamics in a material specimen. Based on this, I will
discuss the notion of Lipschitz deformation distance between integral
currents, which arises physically as a (simplified) measure of
dissipation. In particular, I will explain its relation to the
boundaryless Whitney flat metric.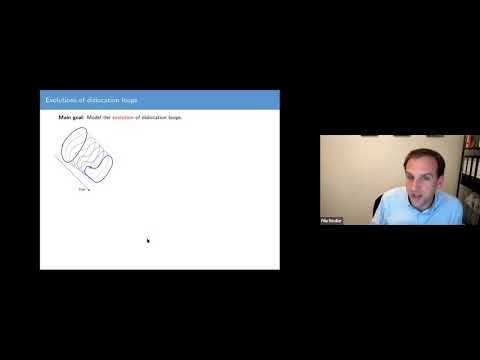
I will present aspects of a theory of space-time integral currents
with bounded variation in time. This is motivated by a recent model
for elasto-plastic evolutions that are driven by the flow of
dislocations (this model is joint work with T. Hudson). The classical
scalar BV-theory can be recovered as the 0-dimensional limit case of
this BV space-time theory. However, the emphasis is on evolutions of
higher-dimensional objects, most notably 1D loops moving within 3D
domains (i.e., the codimension 2 case), which corresponds to
dislocation dynamics in a material specimen. Based on this, I will
discuss the notion of Lipschitz deformation distance between integral
currents, which arises physically as a (simplified) measure of
dissipation. In particular, I will explain its relation to the
boundaryless Whitney flat metric.

FilipRindlerSpace-time

MUST HEAR BEFORE IT’S TOO LATE! Leading Pastor Drops Eerie Report About What’s About To Hit America!
















![Vocal student Reacts to Dimash - Love is like a dream - [ RUSSIAN SUBTITLES] Димаш Кудайберген](https://ytimg.googleusercontent.com/vi/PmsBn0gOe64/mqdefault.jpg)

